GLAET Syllabus 2025 & GLA University Entrance Test Pattern: Candidates who are searching for the GLAET Syllabus 2025 can refer to this article. And, the officials of the GLA University will be held the examination. So, all the applicants need to download the syllabus for the GLA University Entrance Test. Moreover, we have gathered the particulars of the GLA University Entrance Test Pattern 2025 and arranged it on this page. Therefore, all the competitors need to visit this article to prepare for the examination. Moreover, we have arranged the GLA Entrance Test Syllabus 2025 in PDF format. Thus, the contenders can click the given link to download the GLAET Syllabus 2025. In addition to this, refer to the below sections to know the contents to prepare for the test.
GLAET Syllabus 2025 – Details
| Name Of The Organization | GLA University |
| Name Of The Examination | GLA University Entrance Test (GLAET) |
| Category | Entrance Exam Syllabus |
| Official Website | gla.ac.in |
GLA University Entrance Test Pattern 2025
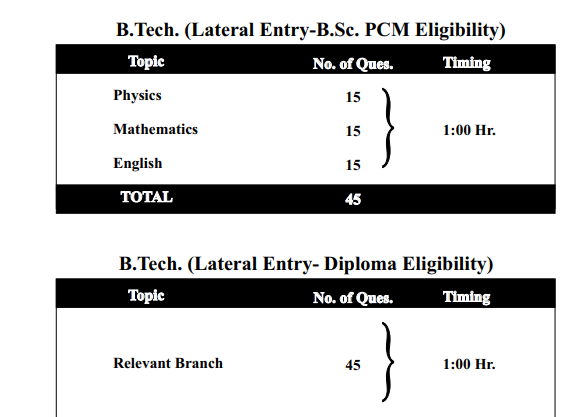
For B.Tech:
| Name of the Subject | No of Questions | Total Time |
| English | 20 Questions | 2 hour (120 minutes) |
| Maths | 45 Questions | |
| Physics | 20 Questions |
For B.Pharm:
| Name of the Subject | No of Questions | Total Time |
| English | 10 Questions | 1 hour 30 minutes |
| Maths/ Biology | 20 Questions | |
| Physics | 15 Questions | |
| Chemistry | 30 Questions |
For D.Pharm:
| Name of the Subject | No of Questions | Total Time |
| English | 10 Questions | 1 hour |
| Maths/ Biology | 10 Questions | |
| Physics | 05 Questions | |
| Chemistry | 20 Questions |
For B.com and BBA:
| Name of the Subject | No of Questions | Total Time |
| English | 10 Questions | 1 hour |
| Maths/ Biology | 10 Questions | |
| Reasoning | 10 Questions | |
| General Knowledge | 10 Questions |
For BCA:
| Name of the Subject | No of Questions | Total Time |
| English | 10 Questions | 1 hour |
| Maths | 15 Questions | |
| Reasoning | 10 Questions | |
| General Knowledge | 10 Questions |
For B.Sc:
| Name of the Subject | No of Questions | Total Time |
| Zoology | 17 Questions | 1 hour |
| Chemistry | 11 Questions | |
| Botany | 17 Questions |

Download GLAET Syllabus 2025 PDF
From these sections, applicants can download the GLAET Syllabus 2025. Moreover, aspirants can click on the link to gather the syllabus for the GLA University Entrance Test. And, the syllabus is different for the various courses. Therefore, all the contenders need to check the syllabus based on their course. Furthermore, students need to wait for few more days to know about the negative marking of the test. So, the participants need to stay tuned to this post to know the frequent updates. Based on the course, candidates need to check the GLAET Syllabus 2025 and practice all the topics. In addition to this, contenders need to answer the questions in the exam based on the negative marking. Therefore, the students need to practice all the topics without leaving any topic mainly.
Mathematics
Algebra
- Functions: Types of functions – Definitions – Inverse functions and Theorems – Domain, Range, Inverse of real valued functions.
- Mathematical Induction: Principle of Mathematical Induction & Theorems – Applications of Mathematical Induction – Problems on divisibility.
- Matrices: Types of matrices – Scalar multiple of a matrix and multiplication of matrices – Transpose of a matrix – Determinants – Adjoint and Inverse of a matrix – Consistency and inconsistency of Equations- Rank of a matrix – Solution of simultaneous linear equations.
- Complex Numbers: Complex number as an ordered pair of real numbers- fundamental operations – Representation of complex numbers in the form a+ib – Modulus and amplitude of complex numbers –Illustrations – Geometrical and Polar Representation of complex numbers in Argand plane- Argand diagram. Multi-conceptual Problem on the above concepts
- De Moivre’s Theorem: De Moivre’s theorem- Integral and Rational indices – nth roots of unity-Geometrical Interpretations – Illustrations.
- Quadratic Expressions: Quadratic expressions, equations in one variable – Sign of quadratic expressions – Change in signs – Maximum and minimum values – Quadratic inequations
- Theory of Equations: The relation between the roots and coefficients in an equation – Solving the equations when two or more roots of it are connected by certain relation – Equation with real coefficients, occurrence of complex roots in conjugate pairs and its consequences – Transformation of equations – Reciprocal Equations.
- Permutations and Combinations: Fundamental Principle of counting – linear and circular permutationsPermutations of ‘n’ dissimilar things taken ‘r’ at a time – Permutations when repetitions allowed – Circular permutations – Permutations with constraint repetitions – Combinations-definitions, certain theorems and their applications.
- Binomial Theorem: Binomial theorem for positive integral index – Binomial theorem for rational Index (without proof) – Approximations using Binomial theorem.
- Partial fractions: Partial fractions of f(x)/g(x) when g(x) contains non –repeated linear factors – Partial fractions of f(x)/g(x) where both f(x) and g(x) are polynomials and when g(x) contains repeated and/or non-repeated linear factors – Partial fractions of f(x)/g(x) when g(x) contains irreducible factors
Coordinate Geometry
- Locus: Definition of locus – Illustrations – To find equations of locus – Problems connected to it.
- Transformation of Axes: Transformation of axes – Rules, Derivations and Illustrations – Rotation of axes – Derivations – Illustrations.
- The Straight Line: Revision of fundamental results – Straight line – Normal form – Illustrations – Straight line – Symmetric form – Straight line – Reduction into various forms – Intersection of two Straight Lines – Family of straight lines – Concurrent lines – Condition for Concurrent lines – Angle between two lines – Length of perpendicular from a point to a Line – Distance between two parallel lines – Concurrent lines – properties related to a triangle.
- Pair of Straight lines: Equations of pair of lines passing through origin – angle between a pair of lines – Condition for perpendicular and coincident lines, bisectors of angles – Pair of bisectors of angles – Pair of lines – second degree general equation – Conditions for parallel lines – distance between them, Point of intersection of pair of lines – Homogenizing a second degree equation with a first degree equation in x and y.
- Circle: Equation of circle -standard form-centre and radius equation of a circle with a given line segment as diameter & equation of circle through three non collinear points – parametric equations of a circle – Position of a point in the plane of a circle – power of a point-definition of tangent-length of tangent – Position of a straight line in the plane of a circle-conditions for a line to be tangent – chord joining two points on a circle – equation of the tangent at a point on the circle- point of contact-equation of normal – Chord of contact – pole and polar-conjugate points and conjugate lines – equation of chord in term of its midpoint – Relative position of two circles- circles touching each other externally, internally- common tangents –centers of similitude- equation of pair of tangents from an external point.
- System of circles: Angle between two intersecting circles – Radical axis of two circles- properties- Common chord and common tangent of two circles – radical centre – Intersection of a line and a Circle.
- Parabola: Conic sections –Parabola- equation of parabola in standard form-different forms of parabolaparametric equations – Equations of tangent and normal at a point on the parabola ( Cartesian and parametric) – conditions for straight line to be a tangent.
- Ellipse: Equation of ellipse in standard form- Parametric equations – Equation of tangent and normal at a point on the ellipse (Cartesian and parametric) – condition for a straight line to be a tangent.
- Hyperbola: Equation of hyperbola in standard form- Parametric equations – Equations of tangent and normal at a point on the hyperbola (Cartesian and parametric) – conditions for a straight line to be a tangent- Asymptotes.
- Three Dimensional Coordinates: Coordinates – Section formulae – Centroid of a triangle and tetrahedron.
- Direction Cosines and Direction Ratios: Direction Cosines – Direction Ratios.
- Plane: Cartesian equation of Plane – Simple Illustrations.
Probability
- Random Experiment: outcome, sample spaces.
- Events: Mutually exclusive and exhaustive events. Axiomatic (set theoretic) probability, probability of an event, probability of “Not” and “Or” events.
- Multiplication theorem on probability, conditional probability, independent events, total probability, Baye’s theorem, random variable and its probability, distribution, mean and variance of a random variable.
- Repeated independent (Bernoulli) trials and Binomial distribution
Trigonometry
- Trigonometric Ratios up to Transformations: Graphs and Periodicity of Trigonometric functions – Trigonometric ratios and Compound angles – Trigonometric ratios of multiple and sub- multiple angles – Transformations – Sum and Product rules.
- Trigonometric Equations: General Solution of Trigonometric Equations – Simple Trigonometric Equations – Solutions.
- Inverse Trigonometric Functions: To reduce a Trigonometric Function into a bijection – Graphs of Inverse Trigonometric Functions – Properties of Inverse Trigonometric Functions.
- Hyperbolic Functions: Definition of Hyperbolic Function – Graphs – Definition of Inverse Hyperbolic Functions – Graphs – Addition formulae of Hyperbolic Functions.
- Properties of Triangles: Relation between sides and angles of a Triangle – Sine, Cosine, Tangent and Projection rules – Half angle formulae and areas of a triangle – Incircle and Excircle of a Triangle.
Calculus
- Limits and Continuity: Intervals and neighbourhoods – Limits – Standard Limits – Continuity.
- Differentiation: Derivative of a function – Elementary Properties – Trigonometric, Inverse Trigonometric, Hyperbolic, Inverse Hyperbolic Function – Derivatives – Methods of Differentiation – Second Order Derivatives.
- Applications of Derivatives: Errors and approximations – Geometrical Interpretation of a derivative – Equations of tangents and normals – Lengths of tangent, normal, sub tangent and sub normal – Angles between two curves and condition for orthogonality of curves – Derivative as Rate of change – Rolle’s Theorem and Lagrange’s Mean value theorem without proofs and their geometrical interpretation – Increasing and decreasing functions – Maxima and Minima.
- Integration : Integration as the inverse process of differentiation- Standard forms -properties of integrals – Method of substitution- integration of Algebraic, exponential, logarithmic, trigonometric and inverse trigonometric functions – Integration by parts – Integration by Partial fractions method – Reduction formulae.
- Definite Integrals: Definite Integral as the limit of sum – Interpretation of Definite Integral as an area – Fundamental theorem of Integral Calculus (without proof) – Properties – Reduction formulae – Application of Definite integral to areas.
Differential Equations
Formation of differential equation-Degree and order of an ordinary differential equation – Solving differential equation by i) Variables separable method, ii) Homogeneous differential equation, iii) Non – Homogeneous differential equation, iv) Linear differential equations.
Vector
- Vectors and scalars, magnitude and direction of a vector Direction Cosines and ratios of a vector.
- Types of vector, equal, zero, unit, parallel and collinear vectors. Position vector of a point , negative of a vector, components of a vector, addition of vectors, Scalar multiplication, position vector of a point dividing a line segment in a given ratio.
- Scalar (dot) product of vectors, projection of a vector on a line.
- Vector (cross) product of vectors, Scalar triple product.
- Coordinate axes and Coordinate planes in three dimensions of a point, distance between two points and sectional formula.
Statistics
Mean, Median, and Mode of grouped data (bimodal situation to be avoided). Cumulative frequency graph.
English
- Antonym
- Synonyms
- One Word Substitutions
- Sentence Completion
- Preposition
- Articles
- Spellings
- Common Errors
Physics
Magnetic Effects of Electric Current
- Magnetic field and field lines
- Magnetic field due to a current a) Straight conductor b) Circular loop c) Solenoid
- Fleming’s Right Hand Thumb Rule
- Left Hand Rule
- Electric Motor, Electromagnetic Induction
- Electric Generator and Domestic Electric Circuit
The Human Eye and the Colorful World
- The Human Eye.
- Power of Accommodation
- Defects of Vision and Their correction
- Refraction of Light Through Prism
- Dispersion of light and scattering of light
- Atmospheric Refraction a) Twinkling of Stars b) Tyndall Effect
Light- Reflection and refraction
- Reflection of light
- Spherical Mirrors: Concave and convex
- Image Formation with Ray diagrams.
- Mirror Formula and Magnification
- Refraction of light through Glass Slab and lenses (convex and concave) and Image
- formation by lenses.
- Lens formula and Magnification
- Uses of Mirrors and Lenses
- Power of Lens.
Sources of Energy
- Different forms of Energy.
- Leading to different Sources of Human use: Fossil fuels, solar energy, biogas, wind water
- and tidal energy.
- Renewable and Non-renewable sources.
Management of Natural Resources.
- Conservation and Judicious use of natural resources.
- Forests and Wild life
- Stake holders and sustainable management
- Dams and Water Harvesting
- Cool and Petroleum.
Electricity
- Electric Current and circuit
- Electric potential and potential difference
- Ohm’s Law
- Series and Parallel combination of resistors
- Heating Effect of Electric Current
- Electric Power
- Inter relation between P,V,I and R.
| GLAET Syllabus 2025 – Important Link | |
|---|---|
| Download GLAET Syllabus 2025 & Exam Pattern PDF | Click Here |
Hope, the given page on GLAET Syllabus 2025 is helpful to all the applicants. And, check exams.freshersnow.com to know more updates like Notification, Syllabus, Previous Papers, Admit Cards, and Results.